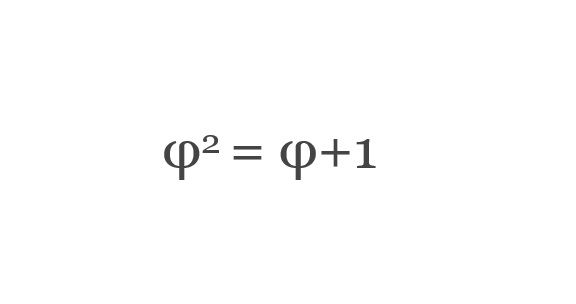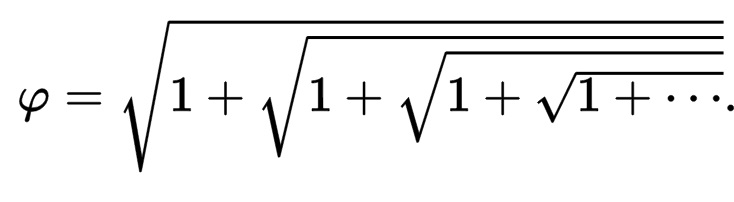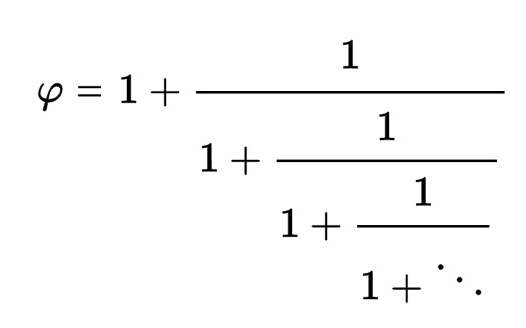Η χρυσή τομή δεν παύει να μας εκπλήσσει (Δρ. Πέτρος Παναγιωτόπουλος, Υπεύθυνος Περιεχομένου Πεμπτουσίας)
2 Απριλίου 2017
Στην αρχαιότητα οι Πυθαγόρειοι πίστευαν στη θεότητα των αριθμών, μιας και τα πάντα στον κόσμο μας διέπονται από αυτούς. Μολονότι οι ίδιοι γνώριζαν μόνο τους φυσικούς αριθμούς (δηλαδή τους θετικούς ακέραιους), υπάρχουν αριθμοί οι οποίοι εμφανίζονται κατά τη μελέτη της φύσης διαρκώς και μερικές φορές αναπάντεχα. Τέτοιοι είναι:
- ο γνωστός μας π = 3,14….
- η βάση των νεπερείων (φυσικών) λογάριθμων e = 2,717….
Οι αριθμοί αυτοί είναι άρρητοι, δεν προκύπτουν δηλαδή ως λόγος (πηλίκο) ακεραίων αριθμών και τα ψηφία τους εκτείνονται απεριόριστα.

Σε ένα κουκουνάρι παρατηρούμε 13 αριστερόστροφες σπείρες και 8 δεξιόστροφες. Αμφότεροι είναι αριθμοί Φιμπονάτσι. Πηγή: Βασίλειος Συμεωνίδης (www.blod.gr)
Ένας άλλος παρόμοιος αριθμός είναι ο φ = 1,618…, γνωστός και ως “χρυσή τομή”. Είναι ένας αριθμός που επίσης εμφανίζεται στη φύση και συνδέεται με την αισθητική.
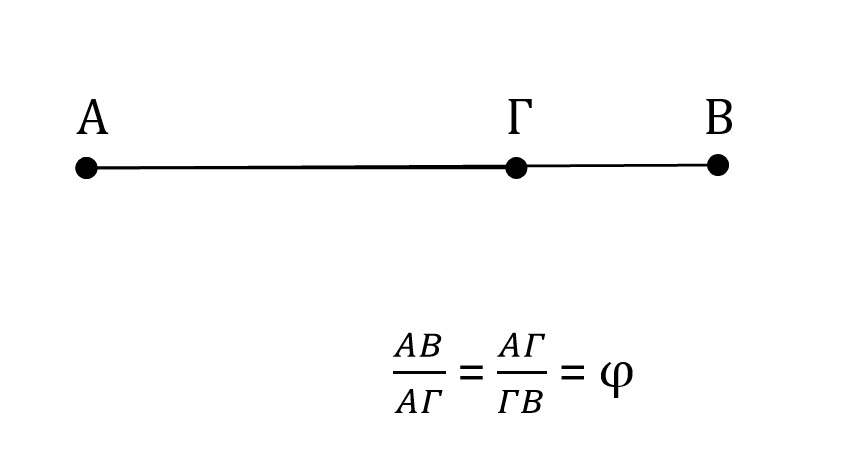
Ο πρώτος που έκανε λόγο για τη χρυσή τομή, ήταν ο Ευκλείδης, ο οποίος εντόπισε το σημείο στο οποίο θα πρέπει να “κόψουμε” ένα ευθύγραμμο τμήμα, ώστε να προκύψει μία εντυπωσιακή αναλογία: ο λόγος όλου του τμήματος προς το μεγαλύτερο κομμάτι του να είναι ίσος με το λόγο του μεγαλύτερου κομματιού προς το μικρότερο.
Αντίστοιχα, λέμε ότι δύο ποσότητες α και β βρίσκονται σε “χρυσή αναλογία”, αν ισχύει η σχέση: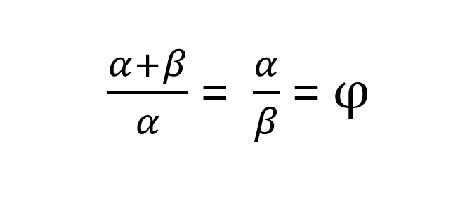 Ο Ευκλείδης δεν το ονόμασε “χρυσή τομή”, αλλά “μέσο και άκρο λόγο”. Την ονομασία “χρυσή τομή” έδωσε το 19ο αι. ο Μάρτιν Ωμ, ενώ ο φίλος του Λεονάρντο Ντα Βίντσι, Λούκα Πατσιόλι (15ος-16ος αι.), την είχε ονομάσει “θεϊκή αναλογία” για την εφαρμογή της στην αρχιτεκτονική. Μάλιστα, ο Γερμανός φυσικός και πειραματικός ψυχολόγος Γκύσταβ Φέχνερ το 19ο αι. πραγματοποίησε έρευνες στις οποίες έδειξε ότι η εφαρμογή της χρυσής τομής σε γεωμετρικά σχήματα προσφέρει αίσθημα αρμονίας. Γεγονός είναι πάντως ότι η χρυσή τομή εμφανίζεται σε πολλές γεωμετρικές κατασκευές (λ.χ. στα σημεία τομής των διαγωνίων ενός κανονικού πενταγώνου).
Ο Ευκλείδης δεν το ονόμασε “χρυσή τομή”, αλλά “μέσο και άκρο λόγο”. Την ονομασία “χρυσή τομή” έδωσε το 19ο αι. ο Μάρτιν Ωμ, ενώ ο φίλος του Λεονάρντο Ντα Βίντσι, Λούκα Πατσιόλι (15ος-16ος αι.), την είχε ονομάσει “θεϊκή αναλογία” για την εφαρμογή της στην αρχιτεκτονική. Μάλιστα, ο Γερμανός φυσικός και πειραματικός ψυχολόγος Γκύσταβ Φέχνερ το 19ο αι. πραγματοποίησε έρευνες στις οποίες έδειξε ότι η εφαρμογή της χρυσής τομής σε γεωμετρικά σχήματα προσφέρει αίσθημα αρμονίας. Γεγονός είναι πάντως ότι η χρυσή τομή εμφανίζεται σε πολλές γεωμετρικές κατασκευές (λ.χ. στα σημεία τομής των διαγωνίων ενός κανονικού πενταγώνου).

Στο ηλιοτρόπιο (αλλά και σε άλλα σύνθετα λουλούδια, π.χ. σε μια μαργαρίτα) σχηματίζονται επίσης δεξιόστροφες και αριστερόστροφες ελικοειδείς καμπύλές, οι οποίες είναι σε πλήθος διαδοχικοί αριθμοί της ακολουθίας Φιμπονάτσι! Πηγή φωτο: wikimedia commons
Υπάρχει η εντύπωση ότι πριν από τον Ευκλείδη η χρυσή τομή ήταν γνωστή στους Πυθαγόρειους (συναντάται στην πεντάλφα τους), στον Πλάτωνα, στην αρχαία ελληνική μουσική, στην κατασκευή του Παρθενώνα [1], των αρχαίων θεάτρων αλλά και των Πυραμίδων. Αντίστοιχα, υποστηρίχθηκε ότι χρησιμοποιήθηκε και αργότερα, στη ζωγραφική και τη μουσική της Αναγέννησης ή και στη σύγχρονη αρχιτεκτονική (π.χ. το κτίριο του ΟΗΕ). Ωστόσο, δεν έχει αποδειχθεί αν πρόκειται για συνειδητή εφαρμογή της αναλογίας, για σύμπτωση ή για εκ των υστέρων εφαρμογή μεταγενέστερων γνώσεων. Είναι πάντως βέβαιο, ότι σύγχρονοι μουσικοί και αρχιτέκτονες χρησιμοποιούν εν γνώσει και συστηματικά τη χρυσή τομή στο έργο τους.
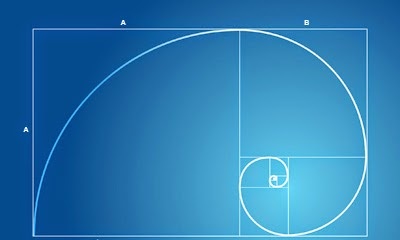
Ισογώνια ή λογαριθμική σπείρα. Προκύπτει από ένα ορθογώνιο παραλληλόγραμμο στο οποίο ο λόγος της βάσης προς το ύψος έχουν χρυσή αναλογία. Στη συνέχεια, στο κάθε τετράγωνο που προκύπτει μέσα στο παραλληλόγραμμο, σχεδιάζεται ένα τεταρτημόριο κύκλου με ακτίνα ίση με την πλευρά του τετραγώνου. Αν οι διαστάσεις ήταν αριθμοί της ακολουθίας Φιμπονάτσι, προκύπτει η ελάχιστα διαφορετική σπείρα Φιμπονάτσι
Εντυπωσιακή είναι οπωσδήποτε η σύνδεση της χρυσής τομής με την ακολουθία Φιμπονάτσι. Αυτή είναι η σειρά των αριθμών 0, 1, 1, 2, 3, 5, 8, 13, 21, … στην οποία κάθε αριθμός προκύπτει από το άθροισμα των δύο προηγούμενων [2]. Διαπιστώθηκε λοιπόν [3], ότι το πηλίκο κάθε αριθμού προς τον προηγούμενό του, τείνει να γίνει φ, όσο μεγαλώνουν οι αριθμοί (1/1=1, 2/1=2, 3/2=1,5, 5/3=1,666…, 8/5=1,6, 13/8=1,625, 21/13=1,615…, 34/21=1,619…, 55/34=1,617…, 89/55=1,618….).
Η εφαρμογή της χρυσής τομής ή αντίστοιχα των αριθμών Φιμπονάτσι στη φύση έχει εντοπιστεί πάντως στη φυλλοταξία (δηλαδή στη θέση των φύλλων σε ένα φυτό), στα φράκταλς (αυτοόμοια σχήματα), στον πολλαπλασιασμό των μελισσών και σε πάρα πολλά σημεία των μαθηματικών [4].
Επιστρέφοντας, στις πολλές αμιγώς μαθηματικές ιδιότητες της χρυσής τομής, γνωρίζουμε για παράδειγμα πως όταν αυτή αυξάνεται κατά μία μονάδα, προκύπτει το τετράγωνό της, δηλαδή ισχύει[5]
Πρόσφατα δημοσιοποιήθηκε μία ακόμη ιδιότητα της χρυσής τομής. Στην τελετή απονομής του βραβείου Abel[6] 2017 στο Γάλλο Ιβ Μεγιέ, μίλησε για το έργο του Mεγιέ και ο μαθηματικός Tέρι Τάο. Στην ομιλία του ανέφερε ότι οι δυνάμεις φ, φ2, φ3, … της χρυσής τομής, βρίσκονται αναπάντεχα πολύ κοντά σε ακέραιες τιμές. Για παράδειγμα η τιμή φ11 = 199,005… βρίσκεται πολύ κοντά στον ακέραιο αριθμό 199!
Λέγεται ότι ο πολυεπιστήμονας (και πιστός χριστιανός) Μπλεζ Πασκάλ έλεγε πως “ο άνθρωπος αδυνατεί να δει την ανυπαρξία από την οποία προέρχεται όσο και το άπειρο που τον καταβροχθίζει”. Εμείς ας αρκεστούμε να πούμε ότι τα θεία μεγαλεία είναι τόσα πολλά μέσα στην κτίση, που έχουμε πάρα πολλά ακόμη να μάθουμε για τη σοφία με την οποία ο Δημιουργός προίκισε τον κόσμο μας.
[1] Το σύμβολο φ δόθηκε στη χρυσή τομή τον 20ό αι. από το Μαρκ Μπαρ, από το πρώτο γράμμα του γλύπτη Φειδία.[2] Προέκυψε από ένα πρόβλημα που είχε θέσει ο Φιμπονάτσι (Λεονάρντο της Πίζας, 12ος-13ος αι.): Αν έχουμε σε έναν απόλυτα κλειστό χώρο ένα ζευγάρι κουνέλια, πόσα κουνέλια θα έχουμε σε ένα χρόνο, δεδομένου ότι κάθε μήνα το ζευγάρι γεννά ένα νέο ζευγάρι και κάθε ζευγάρι γίνεται αναπαραγωγικά ώριμο το δεύτερο μήνα της ζωής του;
[3] Από το γνωστό αστρονόμο Γιόχαν Κέπλερ (16ος-17ος αι.).
[4] Για αρκετούς εφαρμόζεται και στις αναλογίες του ανθρώπινου σώματος αλλά και στην οικονομία. Μάλιστα υπάρχει και μία τριμηνιαία επιθεώρηση, η “Fibonacci Quarterly”, η οποία εκδίδεται ανελλιπώς από το 1963 μέχρι σήμερα και περιλαμβάνει επιστημονικές μελέτες για τις ιδιότητες της ακολουθίας αυτής! Μάλιστα, το 1968 εκδόθηκαν 3 έκτακτα τεύχη του περιοδικού, για να ανταποκριθούν στη συσσώρευση χειρογράφων που
[5] Οι αριθμοί που έχουν την αντίστοιχη ιδιότητα για τον κύβο, αντί για τετράγωνο ονομάζονται “πλαστικοί”. Για έναν πλαστικό αριθμό P, δηλαδή, όταν αυξάνεται κατά μία μονάδα, ισούται με τον κύβο του – με άλλα λόγια ισχύει:
[6] Διεθνές Βραβείο Μαθηματικών, που απονέμεται από το βασιλιά της Νορβηγίας. Για πολλούς θεωρείται ως το “Νόμπελ των Μαθηματικών” – άλλοι ωστόσο εκτιμούν ότι αυτό είναι το Μετάλλιο Φιλντς.

Όστρακο ναυτίλου. Η γεωμετρία του πιστεύεται ότι σχετίζεται με τη λογαριθμική σπείρα. Πηγή: wikimedia commons
Πηγές:
Howard Εves, Μεγάλες στιγμές των Μαθηματικών, τόμ. 1, Έως το 1650, μτφ. Μ. Κωνσταντινίδη – Ν. Λιλή, Τροχαλία, Αθήνα 1989
Peter Bentley, Το Βιβλίο των Αριθμών, μτφ. Α. Μιχαηλίδη, Αλεξάνδρεια, Αθήνα 2010